Deep Learning Neural Networks optimaliseren met Optuna
Door Albert Veldman / mrt 2022 / 1 Min

Door Erik Evers / / 4 min

What if we were able to mimic the events inside our brains and use them to increase the capabilities of our computers? What if we could make these machines go through a learning process similar to children learning how to walk? Would you be surprised to know that this is actually possible? Artificial neural networks are inspired by our own human brain and are designed to recognize patterns. Read on to discover more about the structure of artificial neural networks and how we can use them to make our computers learn! This blog will cover neurons, layers, error functions, and backpropagation.
Artificial neurons are based on biological neurons (see figure 1). As you might have learned in high school, a biological neuron fires off signals when it encounters sufficient stimuli. It is able to pass these signals as output to other neurons. Artificial neurons are very similar. It receives one or more input signals and, when activated, passes an output signal to other neurons.
%20(1).png?width=990&name=image%20(12)%20(1).png) Figure 1. Biological and artificial neuron (Source: Deloitte)
Figure 1. Biological and artificial neuron (Source: Deloitte)
Examining artificial neurons in Figure 2 more closely shows that each input has a certain weight attached to it. This weight indicates the significance of the input with regard to the task that the artificial neural network is trying to learn. The product of all inputs and their respective weights are combined and passed as a total input to the neuron.
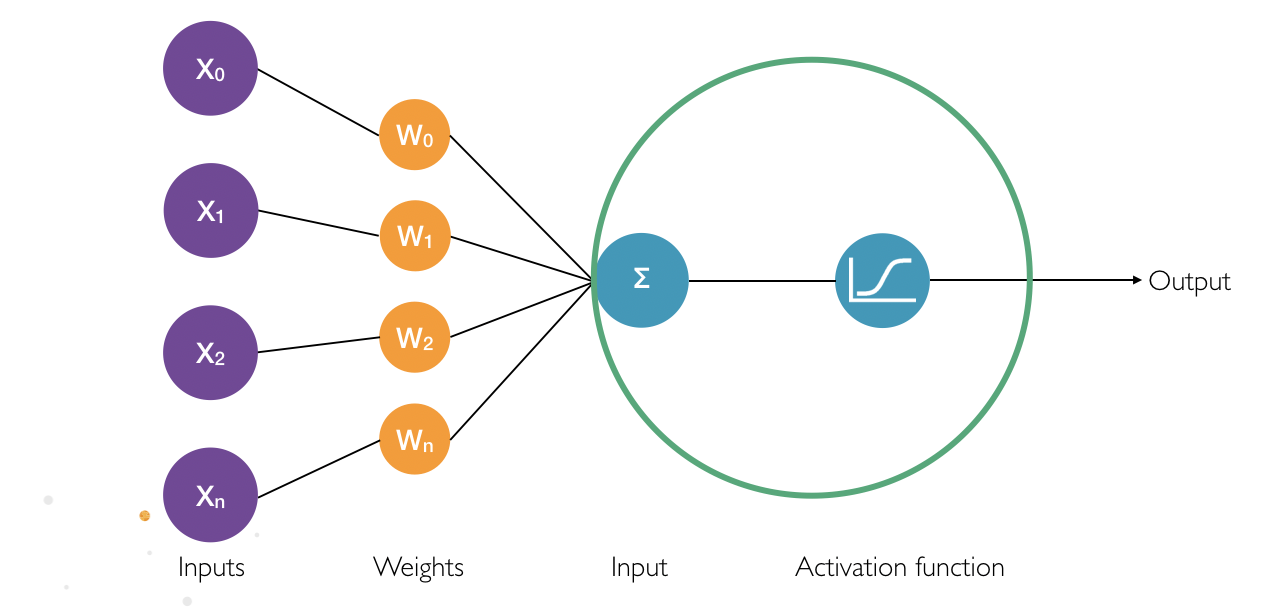
Figure 2. The artificial neuron with inputs
An artificial neuron is a place of computation as input is passed through an activation function. This function determines whether, and to what extent, the signal progresses further into the neural network to affect the ultimate outcome. If an incoming signal progresses further into the network to other neurons, the neuron is activated. There are multiple activation functions, such as the well-known Sigmoid function or the ReLu function (see figure 3 for the latter).
The ReLu function states that if the input is lower than or equal to zero, the output will be zero. If the input is greater than zero, the output will be the same as the input.
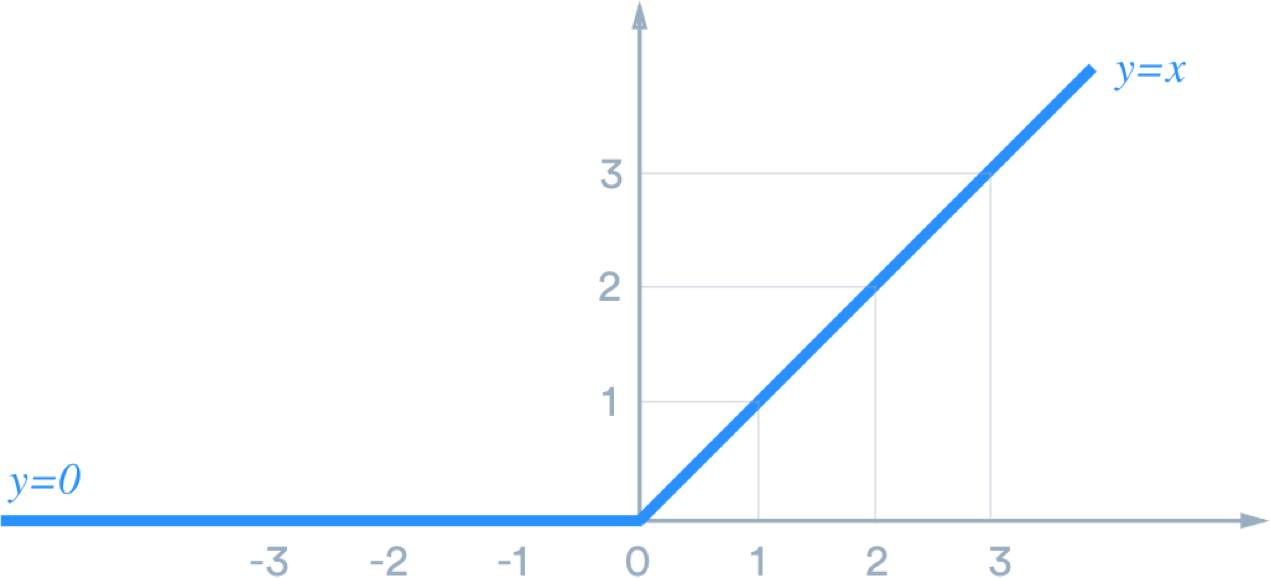 Figure 3. The ReLu function
Figure 3. The ReLu function
Neurons are part of a layer (see figure 4). In this example, we see a layer made up of three blue circles and a layer made up of one purple circle. The neurons may be connected to a neuron in the previous or following layer. The connections between these neurons contain the earlier mentioned weight.
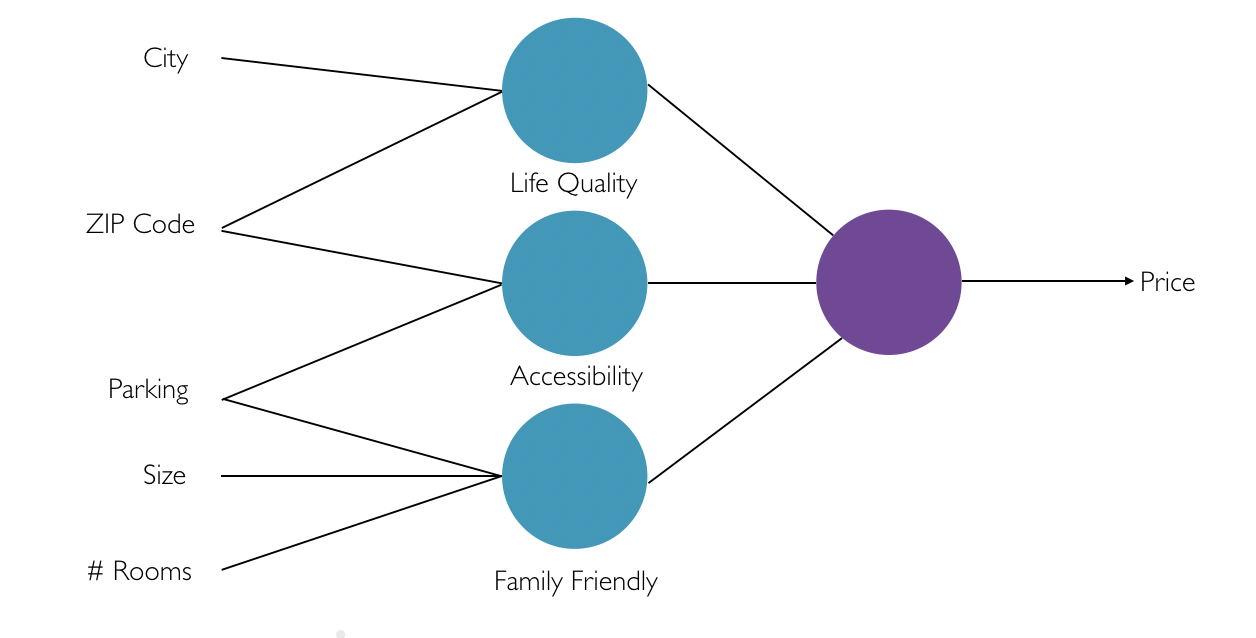
Figure 4. Multiple layers inside a neural network
What kind of processes takes place inside these layers? Let's take the concept of predicting house prices. Humans learn from experience how they can predict house prices by combining multiple input values. Think of input values like:
We learn to make combinations with different input values. For example: combining the city and the ZIP code could say something about the quality of life in that specific neighborhood. The combination of the ZIP code and the number of parking spots could say something about the accessibility of the house. By making these combinations and combining those combinations again, we will eventually be able to predict the price of the house.
This process also takes place inside the artificial neural network. Luckily, the network does most of the work without us explicitly telling it what all the different combinations are. The possible combinations are discovered inside the hidden layers of the network.
In addition to the hidden layers, Figure 5 shows two more layers: input and output layers. The input layer is the first layer of the artificial neural network where input values are received, e.g. the city and ZIP code. The output layer is the last layer of our artificial neural network where an output value is provided, e.g. our house price prediction.
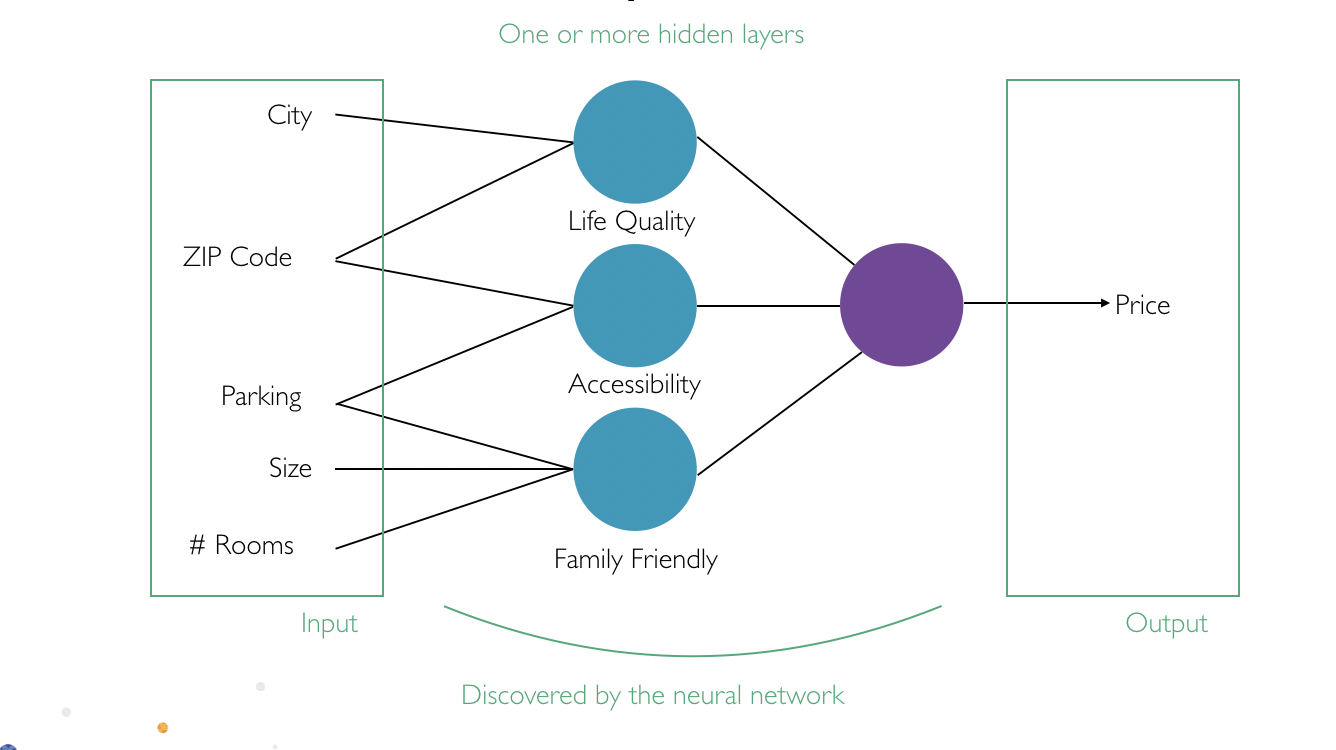 Figure 5. Different types of layers inside the artificial neural network
Figure 5. Different types of layers inside the artificial neural network
So far we've learned that an artificial neural network contains neurons in different layers with weighted connections between them. At the start of the process, passing input values into the network will return incorrect outputs. This is caused by the randomly initialized starting weights of the neurons. How wrong an artificial neural network prediction is can be determined using error functions (also known as loss functions) and labeled examples. To illustrate the use of error functions, let's continue using our example of predicting house prices by passing different values through the neural network (see figure 6).
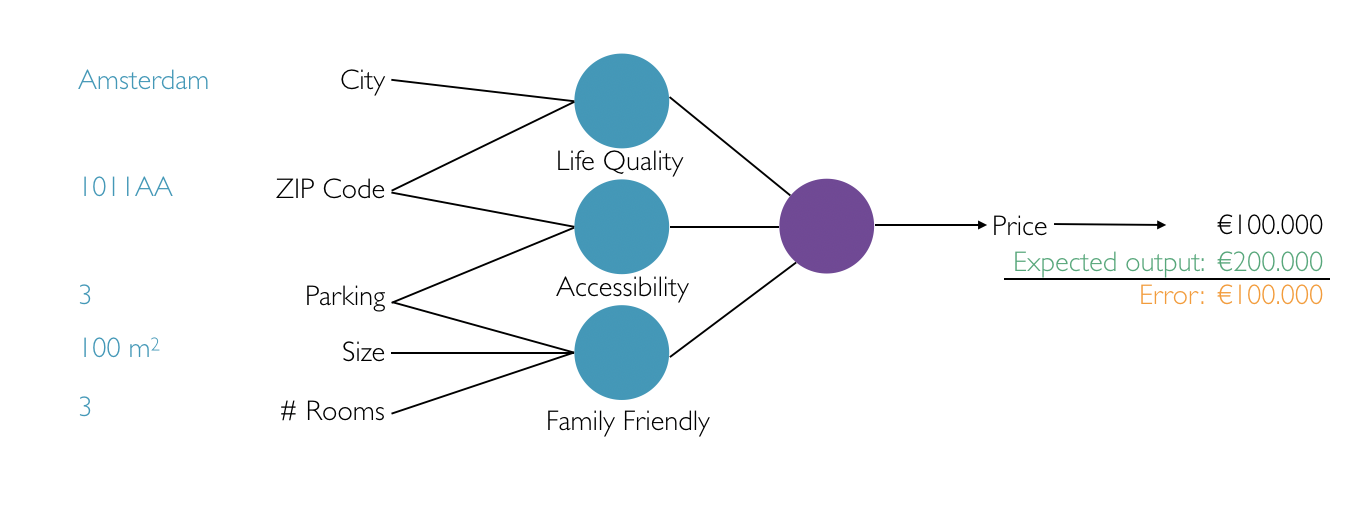
Figure 6. Calculating the error of the artificial neural network
As the values progress through the network, it calculates the input to the neurons by making use of the input values and their corresponding weights. The right output value is determined by applying the activation function to the input value of the neuron. After processing these values, the neural network will eventually give an output of € 100.000. Unfortunately, we know that the prediction must have been € 200.000. The math in this example is easy and we can see that our network has an error of € 100.000 (the difference between the expected output and actual output). There are a number of error functions available which are slightly more complex than just calculating the difference between the expected and actual output. For example, you can use the Mean Squared Error function, which measures the average of the squares of the errors.
After calculating the error of the network, the next step is to optimize the network. This will minimize the error and the actual output will come closer to the expected output. The following paragraph explains how to do this by using the calculated error.
Neural networks can be optimized by applying backpropagation. During this process, we are going to backtrack through the neural network from the output layer, onto the hidden layers and to the input layer of the network. The assigned weight of each connection is updated by using the calculated error. Linear algebra determines the adjustments needed. For example, a partial derivative is determined. If you want to learn more about backpropagation and the mathematical calculations that are applied, I recommend reading Matt Mazur's blog. His blog provides a step-by-step backpropagation example.
Altering the weights will cause chain reactions inside the artificial neural network. The computations inside the network change as a different weight will change the input of the neuron. A new input will change the output of the applied activation function. Ultimately, this leads to a new output value. This process is repeated until the lowest possible error is achieved.
As backpropagation relies on linear algebra, the input values to the network must be numerical. Consequently, this means that values like 'Amsterdam' have to be converted to a numerical representation. A common example of converting an input to a numerical representation is converting an image into its RGB-values. Or, if the image is in black and white, by using the numerical value of the brightness of each pixel.
Artificial neural networks can be used in deep learning. The next blog in this series will dive further into using neural networks with deep learning to train your own image classifier! Stay tuned :-)

| Software Development
Door Erik Evers / okt 2024
Dan denken we dat dit ook wat voor jou is.